A proportion is a fundamental mathematical concept that plays a crucial role in a wide range of applications beyond mathematics and science. It is defined as an equation that represents two given ratios equal to each other. This concept is particularly essential in real-world scenarios, such as cooking, finance, and even art. For instance, when following a recipe to bake a cake, the right balance of ingredients is crucial for a successful outcome. Here, proportions help maintain the correct ratio of ingredients like flour, sugar, eggs, and butter.
Understanding proportions is crucial when working with interest rates, investments, and loans in the world of finance. It enables people and organizations to decide wisely how to use their financial resources. Additionally, artists frequently use proportions in their work to make sculptures and compositions that are visually pleasing, making sure that the pieces are balanced and beautiful.
Example of proportionality:
Consider an example of a train, a train covers 100 km per hour, and the time taken by it to cover the distance is the same as 500 km for 5 hours. We can write 100 km/hr = 500 km/5 hrs. Here, 100 km/hr and 500 km/5 hrs are two ratios, and their equality is a proportion. Proportions play a fundamental role in mathematics and real-world applications. They help us solve various problems involving ratios and relationships between quantities. In this case, the proportionality between distance and time is evident, as the train covers 100 km in one hour, and this rate remains consistent. Proportions are valuable tools in solving problems related to scaling, comparing quantities, and making predictions. Whether in mathematics, science, or everyday life, proportions enable us to establish equivalences and understand the relationships between different quantities, making them a crucial concept in problem-solving and decision-making processes.
Application of proportion:
In many facets of our daily lives, proportion plays a key role in helping us solve problems and make decisions in a variety of contexts. Proportion is an essential instrument for conducting financial transactions and assessing investment prospects in the world of business. Whether you’re determining the optimal pricing strategy for a product or analyzing financial ratios, proportion aids in achieving balance and profitability.
Cooking is another area where proportion is paramount. Precision in ingredient ratios is essential to create delicious and consistent dishes. Whether it’s measuring the right proportion of ingredients for a cake or adjusting the seasoning for a stew, understanding proportion ensures culinary success.
Moreover, real-life scenarios are rife with proportional relationships. Whether you’re calculating the rate of speed during a road trip (distance over time) or comparing prices for different materials (rupees per meter), ratios and proportions simplify complex problems and enable efficient decision-making. In essence, proportion serves as a valuable bridge for comparing and comprehending diverse quantities and their relationships.
Many students get confused about the difference between ratio and proportion. These can easily be understood with the help of examples:
Take 3/5 as a ratio and the proportion statement is 15/25 =3/5. Solving this proportional statement, we get:
15/25 =3/5
Cross-multiply them we get
15x 5 = 25 x 3
75 = 75
If students are still not able to solve proportions they can use calculator-online.net
A ratio is a relationship between two quantities such as a:b, here b should not be equal to 0. One more example: The ratio of 2 to 4 can be represented as 2:4 = 1:2. And we can say this statement is a proportion.
How do you solve proportions?
There are two ways to solve a proportion. Number one is simply cross multiplying, and the other uses the mean extreme property. According to the mean extreme property, the cross product of a proportion is equal to the product of the means and the product of the extremes. In mathematical terms, if you have a proportion like a/b = c/d, where a, b, c, and d are numbers, you can find that ad = bc. This property allows you to solve proportions by equating the cross products. For example, if you have 2/3 = x/6, you can cross multiply to get 2 * 6 = 3 * x, which simplifies to 12 = 3x. Then, you can solve for x by dividing both sides by 3, yielding x = 4. So, the mean extreme property is a valuable tool in solving proportions and is a fundamental concept in mathematics.
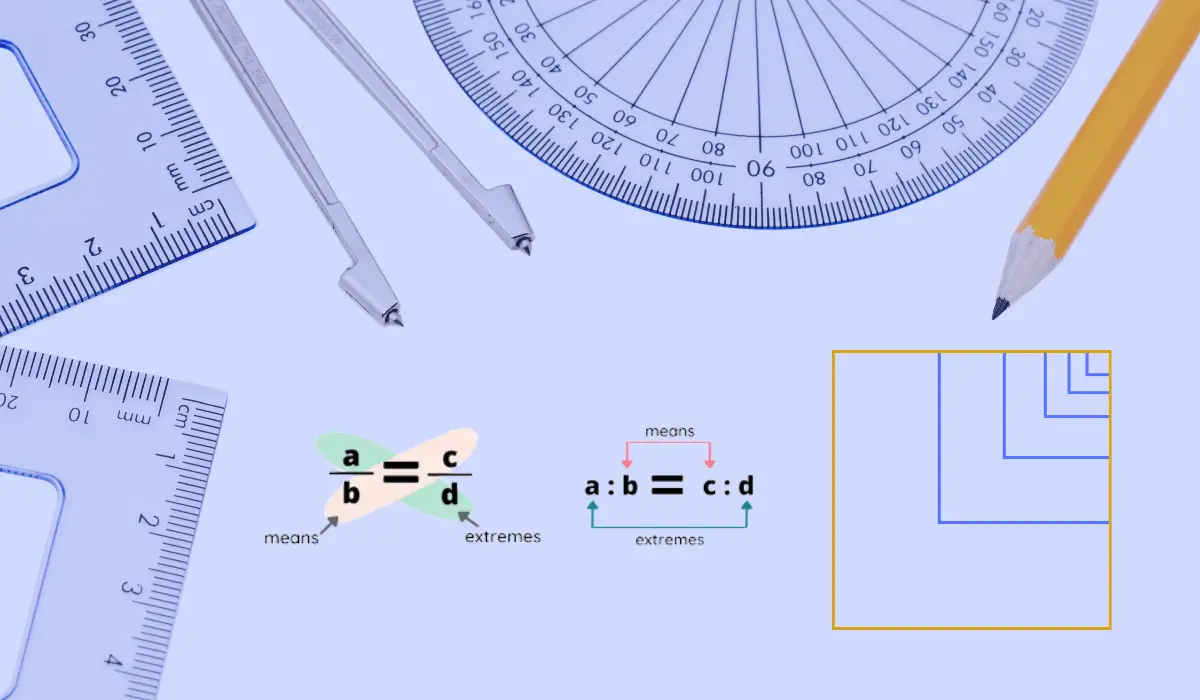
What are the means and extremes in proportion?
Proportions expressed in the form of a:b = c:d are a fundamental concept in mathematics, allowing us to establish relationships between quantities. They enable us to compare values, making them a valuable tool in various real-world applications. The terms on the outer edges, a and d, known as the extremes, hold a special significance as they represent the endpoints of the proportion. In contrast, the inner terms, b and c, referred to as the means, provide the intermediate values in the comparison.
One crucial property of proportions is that the product of the extremes (ad) is always equal to the product of the means (bc). This property forms the basis for solving various mathematical and practical problems involving proportions. Whether you’re scaling recipes in the kitchen, calculating distances on maps, or determining the equivalent values in financial ratios, understanding and utilizing proportions is indispensable. By recognizing this mathematical principle, we can effortlessly identify and solve proportion-related questions across diverse fields, making our lives more manageable and mathematically enriching.
Why is proportion so important?
If you have a variable in your proportion, you can cross-multiply and get an equation that is easier to solve.
Example 1
Solve for x.
x/9 = 2/3
x=2/3* 9
x= 6
For simple equations, manually solving proportions is more accessible and straightforward. It often involves cross-multiplying and basic arithmetic operations to determine the unknown variable. However, when dealing with more complex equations or proportions that involve intricate algebraic expressions, it can be time-consuming and prone to errors. This is where our Proportion Calculator comes to the rescue. Our innovative tool is designed to handle complex proportion problems effortlessly. You can use the calculator to automatically complete the calculations and get the precise answer for the missing variable by entering the known values and the proportion. This reduces the possibility of math errors while also saving you significant time. Whether you’re a student grappling with math homework or a professional working on intricate ratios, our Proportion Calculator is your reliable companion for accurate and efficient proportion problem-solving.
Conclusion:
Proportion is simply a mathematical comparison between two numbers. More specifically, if two ratios are increasing or decreasing directly, they are said to be in direct proportion. This concept is fundamental in various fields of mathematics and real-world applications. Proportions are commonly represented by the symbol “::” or the equal sign “=” to denote their equality. Understanding proportions is essential in solving a wide range of problems, from basic arithmetic to complex statistical analysis.
Proportions find extensive use in diverse areas such as economics, physics, engineering, and even art. In economics, they help analyze cost structures and revenue relationships, aiding businesses in making informed decisions. In physics, proportions are employed to understand the behavior of physical quantities like force and acceleration. Engineers rely on proportions when designing structures to ensure stability and functionality. Even in art, proportions play a crucial role in achieving balance and harmony in compositions.
To make these calculations easier, Proportion Calculators are readily available, simplifying the process of finding and working with proportions in numerous applications, making it an indispensable tool for both students and professionals alike.